XRDP- HowTo Custom install on Ubuntu 16.04.3 with Unity Interface (install-xrdp-1.9.1.sh)

Griffon

  The script hereafter is outdated and has been replaced by a newer version.  Please Check the Download page for latest version.

 

Hello World, 

As you can see, we are quite active lately. We are trying to catch up with all the information we should have been providing a little bit sooner but we are overloaded by work and we are travelling as well which make it difficult to blog and post good article. In this post, we are sharing the updated version of the install-xrdp.sh script.  As you probably know now, Ubuntu 16.04.3 release has introduced some changes at the operating system which has impacted the custom installation procedure of xRDP. 

Background Information

By default, Ubuntu 16.04.x still ships with an old version of xRDP (0.6.x) which provide basic functionalities.  By performing a custom installation, you can get your hands on a more recent xRDP package version (0.9.x) which provides new features such as

  • new xrdp backend server component (xorgxrdp) which makes obsolete the use of VNC server components
  • Clipboard support
  • Drives Redirection  support 

To easy the installation and provide some level of automation, we have been providing a nice little script that automate the installation of the xRDP and configure your system so you can connect to your favorite Unity Desktop through remote connection.  The latest version of the script (install-xrdp-1.9.sh) was working fine until the release of Ubuntu 16.04.3.  This release has introduced a small change that has broken the custom installation process for xRDP.   

Based on the feedback of our user community and our investigation, we have identified some bugs or some change behavior in the Ubuntu 16.04.3 release. You can find more information about these changes in behavior and bugs in the following posts 

Based on the information and findings of these posts, we have updated the install script and we are providing it here..

The Custom Installation Script – Version 1.9.1

Overview

The version 1.9.1 script has been re-worked (and maybe we should label it version 2.0).  It has been updated quite quickly and we didn’t got the time to test intensively but we think that the changes introduced in this version will work on most of the cases. 

Assumptions

Before running this script, be aware of the following assumptions

  • We have tested the script on Ubuntu 16.04 Update 3 (and not on any other Ubuntu Flavors!!!)
  • No additional desktop interface has been installed. Unity Desktop will be the default interface in the remote sessions
  • We have performed the test on a Virtual Machine running on Hyper-V Server and Virtual box 
  • This script should be run only on Ubuntu 16.04.3 (so far) as we have not tested it on higher version. 
  • This script configure the .xsession file for a single user. (a new post configuring multiple users is coming…)

Prerequisites

We assume that you have internet connection on the Ubuntu machine.  The internet connection is needed to download the latest version xrdp package.  If you are not connected to internet, you can still manually download the xrdp package and modify the install-xrdp.sh script accordingly

The script version 1.9.1

 

Version 1.9.1  has been re-worked a little bit.  We have introduced some minor checks and included the necessary actions to ensure that the fontutil.h file is available for the xorgxrdp compilation process to occur flawlessly.  Hereafter, a quick summary of the changes introduced in the Version 1.9.1 of the script  

  • checking the version of your Ubuntu system.  If you are running something different than Ubuntu 16.04.3, the script will not execute
  • simple check of the desktop interface in use while running the script.  The script will execute only if you have Unity Desktop interface running…. 
  • We download the xrdp binaries first and then download and install the necessary software prerequisites.
  • the script will automatically create the fontutil.h file (we do not enable the proposed repositories because this can be a problem for production environment where developer updates might not be accepted) 
  • the script then compile xrdp package first and then the xorgxrdp package.  A simple error handling is in place in order for you to see fatal errors during the make process 
  • as in the previous versions, the script will create the polkit exception and populate the .xsession file
  • the script configure the Xwrapper.config file automatically so you do not have to edit it
  • the script will create the necessary services for xrdp and start the xrdp service  so you can test your connection without the need of a reboot
  • Finally, the script install the xserver-xorg-core package to overcome possible issues with Virtual machines
  • This version of the script will not restart the machine.  This will allow you to review the installation steps of the script by scrolling up and down your terminal console 

We have updated the script to version 1.9.1 to make it clear that this is the latest currently available version that works…. 

Important Note :

If you copy/paste the script, you might encounter some issues because font formatting might be not maintained during the copy/paste operation. Please ensure that format is  accurate before launching the script. A downloadable version of the script is available at the bottom of the post

Disclaimer : As usual, use this at your own risk !! 

################################################################
# Script_Name : install-xrdp-1.9.1.sh
# Description : Perform an automated custom installation of xrdp
# on ubuntu 16.04.3
# Date : August 2017
# written by : Griffon
# Web Site :http://www.c-nergy.be - http://www.c-nergy.be/blog
# Version : 1.9
# Disclaimer : Script provided AS IS. Use it at your own risk....
##################################################################

#---------------------------------------------------#
# Step 0 - Try to Detect Ubuntu Version.... 
#---------------------------------------------------#
echo
/bin/echo -e "\e[1;32m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\e[0m" 
/bin/echo -e "\e[1;32m Dectecting Ubuntu Version and Desktop in use...\e[0m"
/bin/echo -e "\e[1;32m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\e[0m"

version=$(lsb_release -d | awk -F":" '/Description/ {print $2}')

if [[ $version=*"Ubuntu 16.04"* ]]; then 
echo 
/bin/echo -e "\e[1;37mSupported version detected....proceeding\e[0m" 
/bin/echo -e "\e[1;37mUbuntu Version :$version\e[0m" 
echo
else 
/bin/echo -e "\e[1;31m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\e[0m" 
/bin/echo -e "\e[1;31mYour system is not running Ubuntu 16.04 Edition.\e[0m" 
/bin/echo -e "\e[1;31mThe script has been tested only on Ubuntu 16.04.x...\e[0m" 
/bin/echo -e "\e[1;31mThe script is exiting...\e[0m" 
/bin/echo -e "\e[1;31m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\e[0m" 
echo
exit 
fi

#Checking if Unity Desktop in Use

if [ "$XDG_CURRENT_DESKTOP"="Unity" ] 
then 
echo
/bin/echo -e "\e[1;37mUnity Desktop interface Detected....proceeding\e[0m" 
echo 
else 
/bin/echo -e "\e[1;31m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\e[0m" 
/bin/echo -e "\e[1;31mYour system is not running Unity Desktop Interface.\e[0m" 
/bin/echo -e "\e[1;31mThe script has been written to enable Unity Desktop in remote session...\e[0m" 
/bin/echo -e "\e[1;31mThe script is exiting...\e[0m"
/bin/echo -e "\e[1;31m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\e[0m"
exit 
fi


#---------------------------------------------------#
# Step 1 - Download XRDP Binaries... 
#---------------------------------------------------#

sudo apt-get -y install git
cd ~/Downloads

## -- Download the xrdp latest files
/bin/echo -e "\e[1;32mPreparing download xrdp package\e[0m"
/bin/echo -e "\e[1;32m-------------------------------\e[0m"
echo
git clone https://github.com/neutrinolabs/xrdp.git
/bin/echo -e "\e[1;32mPreparing download xorgxrdp package\e[0m"
/bin/echo -e "\e[1;32m-----------------------------------\e[0m"
echo
git clone https://github.com/neutrinolabs/xorgxrdp.git

#---------------------------------------------------#
# Step 2 - Install Prereqs... 
#---------------------------------------------------#

/bin/echo -e "\e[1;32mInstall PreReqs\e[0m"
/bin/echo -e "\e[1;32m-----------------------------------\e[0m"
echo
sudo apt-get -y install libx11-dev libxfixes-dev libssl-dev libpam0g-dev libtool libjpeg-dev flex bison gettext autoconf libxml-parser-perl libfuse-dev xsltproc libxrandr-dev python-libxml2 nasm xserver-xorg-dev fuse

#---------------------------------------------------#
# Step 3 - create the fontutil.h file... 
#---------------------------------------------------#

/bin/echo -e "\e[1;32mIntegrating fix for fontutil bug in ubuntu\e[0m"
/bin/echo -e "\e[1;32m--------------------------------------------\e[0m"
echo
cat >/usr/include/X11/fonts/fontutil.h <<EOF
#ifndef _FONTUTIL_H_
#define _FONTUTIL_H_

#include <X11/fonts/FSproto.h>

extern int FontCouldBeTerminal(FontInfoPtr);
extern int CheckFSFormat(fsBitmapFormat, fsBitmapFormatMask, int *, int *,
     int *, int *, int *);
extern void FontComputeInfoAccelerators(FontInfoPtr);
extern void GetGlyphs ( FontPtr font, unsigned long count,    
             unsigned char *chars, FontEncoding fontEncoding,    
             unsigned long *glyphcount, CharInfoPtr *glyphs );
extern void QueryGlyphExtents ( FontPtr pFont, CharInfoPtr *charinfo,    
            unsigned long count, ExtentInfoRec *info );
extern Bool QueryTextExtents ( FontPtr pFont, unsigned long count,          
            unsigned char *chars, ExtentInfoRec *info );
extern Bool ParseGlyphCachingMode ( char *str );
extern void InitGlyphCaching ( void );
extern void SetGlyphCachingMode ( int newmode );
extern int add_range ( fsRange *newrange, int *nranges, fsRange **range,
          Bool charset_subset );

#endif /* _FONTUTIL_H_ */
EOF

#---------------------------------------------------#
# Step 4 - compiling... 
#---------------------------------------------------#

# -- Compiling xrdp package first

echo
/bin/echo -e "\e[1;32m-----------------------------------\e[0m"
/bin/echo -e "\e[1;32mXRDP Compilation about to start ! \e[0m"
/bin/echo -e "\e[1;32m-----------------------------------\e[0m"
echo

cd ~/Downloads/xrdp
sudo ./bootstrap
sudo ./configure --enable-fuse --enable-jpeg 
sudo make

#-- check if no error during compilation

if [ $? -eq 0 ]
then 
echo
/bin/echo -e "\e[1;32m-----------------------------------\e[0m"
/bin/echo -e "\e[1;32mMake Operation Successful ! \e[0m"
/bin/echo -e "\e[1;32m-----------------------------------\e[0m"
echo
else 
echo
/bin/echo -e "\e[1;31m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\e[0m"
/bin/echo -e "\e[1;31mError while executing make.\e[0m"
/bin/echo -e "\e[1;31mThe script is exiting...\e[0m"
/bin/echo -e "\e[1;31m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\e[0m"
echo
exit
fi
sudo make install

# -- Compiling xorgxrdp package first

echo
/bin/echo -e "\e[1;32m-----------------------------------\e[0m"
/bin/echo -e "\e[1;32mxorgxrdp Compilation about to start ! \e[0m"
/bin/echo -e "\e[1;32m-----------------------------------\e[0m"
echo
cd ~/Downloads/xorgxrdp 
sudo ./bootstrap 
sudo ./configure 
sudo make

# check if no error during compilation 
if [ $? -eq 0 ]
then 
echo
/bin/echo -e "\e[1;32m-----------------------------------\e[0m"
/bin/echo -e "\e[1;32mMake Operation Successful ! \e[0m"
/bin/echo -e "\e[1;32m-----------------------------------\e[0m"
echo
else 
/bin/echo -e "\e[1;31m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\e[0m"
/bin/echo -e "\e[1;31mError while executing make.\e[0m"
/bin/echo -e "\e[1;31mThe script is exiting...\e[0m"
/bin/echo -e "\e[1;31m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!\e[0m"
echo
exit
fi
sudo make install

#---------------------------------------------------#
# Step 5 - create policies exceptions .... 
#---------------------------------------------------#

cat >/etc/polkit-1/localauthority.conf.d/02-allow-colord.conf <<EOF
polkit.addRule(function(action, subject) {
if ((action.id == “org.freedesktop.color-manager.create-device” ||
action.id == “org.freedesktop.color-manager.create-profile” ||
action.id == “org.freedesktop.color-manager.delete-device” ||
action.id == “org.freedesktop.color-manager.delete-profile” ||
action.id == “org.freedesktop.color-manager.modify-device” ||
action.id == “org.freedesktop.color-manager.modify-profile”) &&
subject.isInGroup(“{group}”)) {
return polkit.Result.YES;
}
});
EOF

#---------------------------------------------------#
# Step 6 - configure Xwrapper file .... 
#---------------------------------------------------#

sudo sed -i 's/allowed_users=console/allowed_users=anybody/' /etc/X11/Xwrapper.config

#---------------------------------------------------#
# Step 7 - Populate the .xsession file .... 
#---------------------------------------------------#
cat >~/.xsession << EOF
/usr/lib/gnome-session/gnome-session-binary --session=ubuntu &
/usr/lib/x86_64-linux-gnu/unity/unity-panel-service &
/usr/lib/unity-settings-daemon/unity-settings-daemon &
for indicator in /usr/lib/x86_64-linux-gnu/indicator-*; 
do
basename='basename \${indicator}' 
dirname='dirname \${indicator}' 
service=\${dirname}/\${basename}/\${basename}-service 
\${service} &
done
unity
EOF

#---------------------------------------------------#
# Step 8 - create services .... 
#---------------------------------------------------#
sudo systemctl daemon-reload
sudo systemctl enable xrdp.service
sudo systemctl enable xrdp-sesman.service
sudo systemctl start xrdp

#---------------------------------------------------#
# Step 9 - install additional pacakge .... 
#---------------------------------------------------#

sudo apt-get -y install xserver-xorg-core

/bin/echo -e "\e[1;32m----------------------------------------------------------\e[0m"
/bin/echo -e "\e[1;32mInstallation Completed\e[0m"
/bin/echo -e "\e[1;32mPlease test your xRDP configuration....\e[0m"
/bin/echo -e "\e[1;32mCheck c-nergy.be website for latest version of the script\e[0m"
/bin/echo -e "\e[1;32mwritten by Griffon - August 2017 - Version 1.9.1\e[0m"
/bin/echo -e "\e[1;32m----------------------------------------------------------\e[0m"
echo

How to Use the Script

Set Execute Right on the script

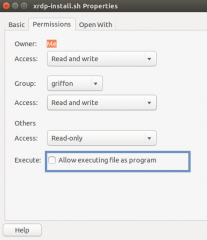
Download the install-xrdp-1.9.1.sh script to your system.  To have it running, the script has to be marked as executable.  To mark a script/file as executable, the following actions needs to be performed 

Right-click on the file, go to properties, then select permissions and tick the box allow executable….

xrdp_custom

Click on Picture for better resolution 

or from the command line, issue the following command

chmod +x  ~/Downloads/install-xrdp-1.9.sh  

Note : Adjust the path where the install-xrdp-1.9.1.sh script to reflect your environment

Execute the script

To execute the script, ensure that internet connection is available (so you can download the necessary packages needed for the installation) and simply open a Terminal console.  In the Terminal console, Browse to the location where the script has been stored and then issue the following command 

sudo ./install-xrdp-1.9.1.sh  

You might be prompted for a password. Provide the password and proceed with the installation.

Wait for completion of the script.  The machine will not reboot automatically when done so you can review the actions performed by the script….

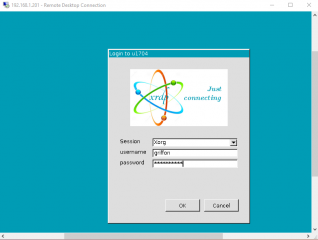
Test your xRDP Infrastructure

At this stage, if everything is working as expected, you should be able to perform a remote desktop session to your Linux machine.  In the xrdp login page (the green background), ensure that Xorg option is selected, provide your user name and password, and you should be able to access your Ubuntu machine.  

U1704_xrdp_3

Click on picture for better resolution

Normally, in the xRDP login page, the keyboard should match the one you are using on your normal computer.  This was not the case in the past and has been fixed with the introduction of the xorgrdp server (it seems).  However, note that within the remote session, the keyboard layout might not match if you are using multiple ones.  This can be easily fixed through the indicator language bar within the xrdp session. Select the proper keyboard layout and you should be good to go….

U1704_xrdp_8

Click on picture for better resolution

The user that has executed the script will be able to remote desktop into Ubuntu and the Unity Desktop will be launched automatically.  In Ubuntu 16.04.3, you can have the same user logged into the console and to the remote session and this scenario would work.  In later version of Ubuntu, it seems that the behavior has changed…(we will investigate a little bit further).  The user will be able to reconnect to an existing session as well and the user will be able to use the clipboard and drives redirection features.. 

Issues detected 

Surprisingly, we have have not really discovered many issues with this configuration so far.  The performance are acceptable over a LAN network.  The interface is quite smooth and we have access to the different applications, we can even change wallpaper while performing the remote session.  The logout process is still a little bit problematic.  You have to go twice through the logout process to have it working..

As in our previous posts, you can try to use the following command line (or make a custom shortcut that users can they use to logout in one step)

ps -ef h | grep xorgxrdp | grep `whoami` | tr -s " " | cut -d " " -f2 | xargs kill -9

 

Download the Script 

Please download the script :  install-xrdp-1.9.zip

Demo

To demonstrate that the script seems to work properly, the quick and dirty video below walk you through the process and shows you that the script should be working as expected 

 

Final Notes

Voila ! The new script version is available and should be working till the next coming Ubuntu updates probably…. We are still hesitant in adapting the script for Ubuntu 17.04 and Ubuntu 17.04 Gnome desktop as starting from these releases, xrdp package 0.9.x is available out of the box and with the xorgxrdp component…. 

If you detected any issues with the script, please drop us a line and we will update it 

Till next time 

See ya

 

50 thoughts on “XRDP- HowTo Custom install on Ubuntu 16.04.3 with Unity Interface (install-xrdp-1.9.1.sh)”

  2. @Mike,

    Euh….your comment seems not to be complete….We would love to know your way of extracting Ubuntu Version….We are always looking for new ways or alternate ways…
    Please repost your comments
    Thank for the visit and your (partial) comments….
    Till next time
    See ya

  3. Unfortunately I enclosed the comment in brackets. Its “lsb_release -d | grep -o 16.04.3”.

    Unfortunately I’m still fighting the xrdp install in Ubuntu 16.04.3. I’m in and can get to the command line but everything runs slow and the background seems to get not update correctly. Anyways I can get to the command line.

    By the way there is a copy error on the file you posted on this page. The error is NOT in the download file. I put some ### signs around the error.

    extern int CheckFSFormat(fsBitmapFormat, fsBitmapFormatMask, int *, int *,
    int *, int *, int *); ### int *, int *, int *); ###
    extern void FontComputeInfoAccelerators(FontInfoPtr);
    #### extern void GetGlyphs ( FontPtr font, unsigned long count, ####
    extern void GetGlyphs ( FontPtr font, unsigned long count,
    unsigned char *chars, FontEncoding fontEncoding,
    unsigned long *glyphcount, CharInfoPtr *glyphs );

    Cheers,

  4. You state “The logout process is still a little bit problematic. You have to go twice through the logout process to have it working.” I believe that this is where the problem lies in Hyper-V and I suspect also in VirtualBox. In a Hyper-V Ubuntu 16.04.3 I can make the connection with the remote desktop. But after the first connection with remote desktop is ended using the logoff script you provided or dropping the connection I can not get back to the log in screen from the Hyper-V manager. I can still remote into the Ubuntu 16.04.3 desktop through the remote desktop connection. That’s it for now. Cheers.

  5. Sorry for repeatedly commenting but I found a way to get my log-in screen back and keep my remote. Unfortunately I’m not exactly sure where the problem lay. This is a shotgun repair

    Ctrl Alt F1 to get into the Ubuntu console- then

    sudo apt-get update
    sudo apt-get install –reinstall ubuntu-desktop
    sudo apt-get install unity # didn’t seem to need this line but I threw it in
    sudo reboot

    Now I can get into the Ubuntu 16.04.3 from the hypervisor (v. 2012) and a Win10 remote desktop connection.

  7. Hi,

    Kudo for the work done, much appreciated. However, is there any chance to make the same tutorial for Kubuntu 16.04.3 with Plasma 5?
    You state very clearly that the above only works for Ubuntu Unity but it’s hard to love that one …

    Thanks in advance for your feedback

  8. After had installed script in my Ubuntu 16.04.3, mouse and keyboard didn’t work in local console.
    Would you check it ?

    Thanks for your job!

  9. I tried running the script renbuar provided without using sudo but on a “sudo reboot” the screen went all wobbly (slow and crashed).
    BTW below is the code I used to get the script to check for Ubuntu version 16.04.3

    uversion=$(lsb_release -d | grep -o 16.04.3)
    if [ $uversion = “16.04.3” ]

    Also I determined that the logoff script provided by Griffon works nicely. It seems gentler than my “pkill -u username”.

    Also my guess at this time is when “sudo apt-get -y install xserver-xorg-core” is run this causes my virtual machine to post errors and also hangup so that virtualbox or MS hypervisor can not logon to the virtual machine through the desktop. I can still rdp into the virtual machines though . My workaround was to
    “sudo apt install –reinstall ubuntu-desktop”. I guess it will involve a hunt through the log files and/or apt-cache package files to determine what the problem is. To Griffon thanks for all the hard work. Cheers!

  10. @Oleg,

    This one is a strange one as the script simply install some packages into your system… Are you running hyper-v, virtualbox virtual machines or physical machines… ?

    Till next time
    See ya

  11. @Mike Rehner,

    Thank for the comments,feedback and technical alternative to detect Ubuntu version….
    based on different feedback received, the script we have made available provide some nice improvements but for some users there are still some issues. When time permit, we will check if we can Improve further the installation script

    Till next time
    See ya

  12. @ionut

    We will try to update the script to include more distribution but this might take some time as we are really busy right now…..
    Thank for the positive feedback and your visit
    Stay tuned for updates
    Till next time
    See ya

  13. @oleg
    Get to the command line either by rdp or doing 2 restarts. Then try this

    sudo apt update
    sudo apt -y install –reinstall ubuntu-desktop
    ###
    # thats 2 each dashes above before reinstall, the html injection checker
    # I believe may change it to one long dash
    ###
    sudo reboot

    Hope that helps you get back to a local connection.

  14. Griffon, your script is correct, but in the picture there are extra lines in the file fontutil.h, correct:
    #include

    extern int FontCouldBeTerminal(FontInfoPtr);
    extern int CheckFSFormat(fsBitmapFormat, fsBitmapFormatMask, int *, int *,
    int *, int *, int *); int *, int *, int *);
    extern void FontComputeInfoAccelerators(FontInfoPtr);
    extern void GetGlyphs ( FontPtr font, unsigned long count,
    extern void GetGlyphs ( FontPtr font, unsigned long count,

  15. @Renbuar;

    Yep, thank for letting us know….We have seen your previous comments but no time to perform the changes…The post has been updated and should be good now…

    Till next time
    See ya

  16. @Griffon, Thanks so much for the script, very useful.

    Could I suggest a change in the script?
    After cloning from the xrdp repos, could you reset to the specific commit that worked for you before starting the build? This will protect your script from unstable/breaking commits that may not have been tested yet by the xrdp devs.

  17. I would like ask questions about Ubuntu Desktop on xrdp.
    1. I can’t install any packages through app Software or Synaptic Package Manager.
    2. I don’t have icons on Menu like All Setting – Appearance – Behavior
    Could you help me?

    Thanks for your job.

  18. @Oleg,

    We didn’t encounter this issue. are you running virtualization solution ? have you checked that the xserver-xorg-core package is installed on your system ?
    Hope this help
    Till next time
    See ya

  19. @Karthikv,
    thank you for your support and your comments. We could indeed try to update the script in order to ensure that it works with the version we have performed the test with
    We will see if this is an option in the future as for the moment we are overloaded by projects, work, travel…so not so much time to blog lately..
    Thank for the suggestions….

    Till next time
    See ya

  20. I ma facing hat @oleg is facing
    After had installed script in my Ubuntu 16.04.3, mouse and keyboard didn’t work in local console.
    Whats the solution ?

  21. After had installed script in my Ubuntu 16.04.3, i connect by xrdp to Unity desktop.
    But i have some troubles:
    1. I can’t install any packages through app Software or Synaptic Package Manager.
    2. I don’t have icons on Menu like All Setting – Appearance – Behavior

    Could you help my?

    Thanks for your job!

  22. @Griffon — Some of @Oleg ‘s problems are due to a lack of elevation prompts, I believe.

    A problem I’m having as well. A good test of this is to download Google Chrome and try to install it through the UI. Remotely, it either hangs or just self-cancels. Locally I’m asked for admin credentials.

    I also get crashes in polkitd and aptd that are new. I believe these may also be related to the elevation problem. I’m sure this is a minor configuration issue, but it’s beyond my admin-fu, for sure.

  23. @Chandra,

    We have not encountered this issue (yet?) and had not time to look into it… IF somebody had already faced this issue, maybe they can share their thoughts, tips, tricks, troubleshooting steps, outcome

    Thank you
    Till next time
    See ya

  24. @Oleg,

    Ok, we never encountered this issue…. and based on comment of Tyler, inside the remote session, when elevation is required, we can see that and proceed with the action…
    We have not fully tested the xrdp on gnome yet… For install packages, try to run from the sudo command line to start software center and see if this is better. If this is the case, then, elevation might be blocking you….

    For the appearance, maybe a typo in the .xsession…. file .. Double check that the commands are correct….
    We will try to have a lookt into it but might take some time we are really busy right now…

    till next time
    See ya

  25. @Tyler,

    Thank you for the input…as we have not encountered the issue, cannot tell…. We will need to check that..however, usually, when performing actions inside remote session requiring elevation we are presented with the login box… so at the moment no clue and cannot infirm/confirm your statement but you might be right

    Thanks for the feedback
    Till next time
    See ya

  26. I’m trying this on a physical Ubuntu Server 16.04.3 machine. I get to the end and can see the green RDP screen. I can enter my credentials, but then the green goes and stays black. After reading your previous posts, here’s the/an error I see via command line
    $ Xorg :10 -auth .Xauthority -config xrdp/xorg.conf -noreset -nolisten tcp -logfile .xorgxrdp.%s.log
    (EE)
    Fatal server error:
    (EE) The ‘-logfile’ option cannot be used with elevated privileges.
    (EE)
    (EE)
    Please consult the The X.Org Foundation support
    at http://wiki.x.org
    for help.
    (EE)

    and xrdp-sesman.log:
    [20170913-20:42:39] [INFO ] A connection received from 127.0.0.1 port 55260
    [20170913-20:42:40] [INFO ] ++ reconnected session: username md, display :10.0, session_pid 2122, ip 128.61.182.100:42502 – socket: 12
    [20170913-20:42:40] [DEBUG] Closed socket 9 (AF_INET 127.0.0.1:3350)

    Any thoughts?

  27. @MD;

    sorry for the delay in response…we have been working abroad and we are just back…
    So, if I read the message, you are trying to generate a log file but with elevated rights…
    So, you should go to your ubuntu, log into the console, open the terminal console and execute the command (with no sudo) and see if this works…..
    Finally, please have a look at the following post (http://c-nergy.be/blog/?p=9433), it s probably outdated but might give you some hints..

    Hope this help
    Till next time
    See ya

  29. @rkantos;

    Thank you for the feedback and the visit…The script was initially used to speed up the xrdp isntallation….We might consider your requests based on our availability and evolution of the Desktop landscape and xrdp packages
    till next time
    See ya

  31. @UbuntuUser,

    as far as i know, this is still work in progress. Some people have tried to make it worked and succeeded but with tricky configuration
    Hope this help
    till next time

    See ya

  32. nice script. It works perfectly. And yes, the version check at the beginning should be adapted. Thanks for your support.

  33. @ecc0o,

    Thank you for the feedback and for visiting our blog…Good to see that this work has some value…. Indeed, value check will be updated as we are moving to new Ubuntu version
    Till next time
    See ya

  34. There are two causes for problems that mouse and keyboard do not work when reboot after install xrdp on VMware Virtual Machine.
    1. You need X.org driver for VMware,
    2. LightDM does not support X.org driver.

    There are two measures.
    1. Install ‘ Vmware-tools’ rather than ‘ open-vm-tools’ .
    2. Use GDM instead of LightDM.

    This will make it work.
    It works my vmware workstation 14 pro.

  36. Hello Griffon,

    Thanks for your awesome articles about xrdp, it really helps !
    This script works perfectly excepts that my launcher is missing and the top bar (logout , links).
    I’m running this on Ubuntu 16.04.3 (not a virtual machine), i tried with your previous scripts same issue.
    Any ideas ?

    Thanks a lot,
    PS: I had to change the first check of your script, “checking version” (uname -n) was returning the name of my computer and not my system release

  37. @MtheMonkey,

    First, the script contains indeed a small error in the OS check..we will updated it and provide the correct version 🙂
    Second about the top bar and the launcher (I m assuming the left side menu in ubuntu), I would definitly check that the .xsession file is populated correctly
    as a test, could you right-click on the desktop then select new terminal and in the terminal issue the command exec unity => do you see a normal ubuntu desktop or do you have an error ?
    Can you check your logs /var/log and ~/.xsession-error files, and see if any hints to find the solution to your problem ?

    Hope this help
    Till next time
    see ya

  38. Hello!
    I just would like confirm.
    Missing top bar (language switch, time,logout) in xrdp.
    Look forward to new version of script with fix this issue.

  39. @Oleg,

    Thank you for the feedback and your visit. As you are not the first one to mention that the top bar does not seem to work, we will need to check the script again and see if things have changed in Ubuntu 16.04 with recent updates…

    Till next time
    See ya

  40. @Oleg,

    We have updated the script to version 1.9.2 (really minor changes) and we can see that the Unity Interface is working as expected. We can see the Top bar and the logout options….
    Did you download the script or simply copy/paste from the blog ?
    Recommended to download the script from the blog

    Hope this help
    Till next time
    See ya

  41. Do you have an update for 16.04.4? I am unable to get this to work and I am wondering if its due to the version.

  42. @Tony,

    we are working on this update and it should be available on Saturday/Sunday….. Sorry for the delay but we are busy busy with projects…
    A little bit of patience… in the mean time, maybe explain what’s not working and what your infrastructure (physical or virtual – if virtual which soft used…)

    Till next time
    See ya

  43. Sorry Griffon, I wasnt being impatient and I understand the delay, I just appreciate the script and the help!

    Its a physical machine, a desktop in my office, that I was simply looking to remote into and preferred (x)RDP and a little googling brought me to your script. I ran it, it ran fine, no errors that I see. When I connect from mstsc.exe on my windows 10 laptop it presents me with the log in screen, after I put in my credentials the screen turns black for a few seconds then disconnects me from the server.

  44. also fyi, the script text above and the actual download link you have on this page appear to be slightly different. I ended up trying the downloadable one first then overwriting it with the version copied from text because I noticed the header was more recent. As other commentor’s have mentioned, I had to remove the version check section as ‘uname -m’ doesnt list kernel version anyway.

  45. @Tony,

    You have been doing the correct thing so far… Indeed, the detection method for the os is a mistake from our side…. We have noticed that since a moment but never had the time to update the script…. will do…..

    sorry for the inconvenience…. the new script will be released tomorrow as we finalizing it

    Till next time
    see ya

  46. @Tony,

    no worries Tony, you are not pushing us…This update was foreseen but we lacking time to do everything we want to on this blog…
    For your issues, can you try the following….. logoff completely from the physical machine and try to connect only to remote session….
    Maybe with this update, you cannot at the same time connect to the console and to the remote session (using the same account)
    If you get a disconnect the first time, this might be expected, try a second time and see if you can connect

    till next time
    See ya

  47. how to revert all changes made by this script? I can’t login to my pc after installation (keyboard not working). Both RDP and physical session are unaviable. In recovery mode after a while keyboard stops working with message “input overrun at /dev/tty1. I have access to ssh, disabled xrdp and xrdp-sesman, but still can’t use phisical keyboard to login.

  48. @syfny-skrypt

    We have noticed that newer installation of xRDP can remove input packages from your system. Can you try to run the following command (through ssh) and see if your keyboard/mouse are back
    sudo apt-get -y install xserver-xorg-input-all

    This topic/remark/issue has been addressed in the following post (http://c-nergy.be/blog/?p=11719)… and the script has been modified accordingly (version 1.9.2) to detect virtualization platform and install this package

    About your question to remove xrdp completely -> Have you looked through the blog ? There is an post explaining how to remove the custom installation (http://c-nergy.be/blog/?p=11454)
    Basically, you simply delete the files and folders placed on your system during the xrdp installation and that’s it…..

    Hope this help
    till next time
    See ya

  49. Worked best for me:
    ps -ef h | grep Xorg | grep xrdp | grep -v grep | grep `whoami` | tr -s ” ” | cut -d ” ” -f2 | xargs kill

Leave a Reply